Welcome back everybody! In this blog I will be talking about hypothesis testing and sharing everything that I have learned.
HYPOTHESIS TESTING
The first thing we should know about is what exactly is hypothesis testing. While it may seem quite obvious from the name itself, it is actually much deeper than what I thought it would be.
Hypothesis testing allows for statistical hypothesis to be proven or rejected through formal procedures.
Statistical hypothesis: an assumption about a population that may or may not be correct.
Hypothesis testing can be used to answer questions such as:
- Is the new material as strong as the old one?
- Is the performance of our product enhanced after undergoing the revamp?
- Is the spare part performing as well as the original part?
In my case I will be conducting an experiment to undergo hypothesis testing for the effects of various factors on a catapult. Frequent readers of my blog will recognise that this is actually the same experiment as my practical for Design Of Experiment.
Conducting The Hypothesis testing
For this experiment, my CPDD practical group have been split into different roles and we will each be conducting hypothesis testing on each of our allocated runs.
Here are our roles and responsibility:
|
Name of heroes
(students) |
Runs |
Factor tested |
|
Ironman (Jia Tong) |
#1 & #3 |
Effect of
projectile weight |
|
Thor (Devin) |
#2 & #4 |
Effect of
projectile weight |
|
Captain America
(Jun Kai) |
#2 & #6 |
Effect of
stop angle |
|
Black Widow (Aminur) |
#4 & #8 |
Effect of
stop angle |
|
Hulk (Ji Hinn –
Me) |
#6 & #8 |
Effect of
projectile weight |
After allocating our roles, we then proceeded to conduct hypothesis analysis using the data we collected before:
I will be using the data for run #6 and #8 and following the formal procedures to conduct hypothesis!
The Question
To determine the effect of projectile weight on the flying distance of the projectile.
Scope of the test
The human factor is assumed to be negligible. Therefore, different user will not have any effect on the flying distance of projectile.
Flying distance for catapult is collected using the factors below: Arm length = 33 cm Projectile weight = 0.88 grams (run #6) and 2.07 grams (run #8) Stop angle = 50 degrees
Step 1: State the statistical hypotheses
Null hypothesis (H0): When the arm length and stop angle of the catapult remain constant at 33 cm and 50 degrees respectively, the distance travelled for projectile weight of 0.88 grams will be the same as a projectile weight of 2.07 grams.
µ6 = µ8
Alternative hypothesis (H1): When the arm length and stop angle of the catapult remain constant at 33 cm and 50 degrees respectively, the distance travelled for projectile weight of 0.88 grams will be further than a projectile weight of 2.07 grams.
µ6 > µ8
Step 2: Formulate an analysis plan
Sample size is 16. Therefore, t-test will be used.
Since the sign of is H1 >, a right-tailed test is used.
Significance level (α) used in this test is 0.05
Step 3: Calculate the test statistic
Mean and standard deviation of run #6
X̄6 = 196.00 cm
S6 = 4.11 cm
Mean and standard deviation of run #8
X̄8 = 174.75 cm
S8 = 2.87 cm
Computing the value of test statistic (t):
Step 4: Make a decision based on result
Type of test
- Left-tailed test [ ], Critical value tα =
- Right-tailed test [✔], Critical value tα = 1.761
- Two-tailed test [ ], Critical value tα/2 =
Following the diagram above, since t = 11.3 and tα = 1.761, t > tα. Therefore, t lies within the rejection area and H0 is rejected.
Conclusion
Inferences made from conclusions
Weight of projectile have an effect on distance travelled
- The lower the weight of projectile, the longer the distance travelled
- The greater the stop angle, the longer the distance travelled




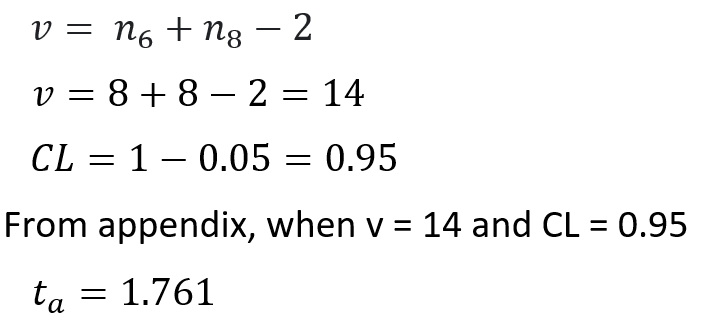


Comments
Post a Comment